This post is meant for people who are just getting started with mechanistic interpretability and have an understanding of the transformer architecture as well as the underlying linear algebra. Maybe you have not yet read the mathematical framework for transformer circuits (MFTC) or have read it but are still confused about some things. I know that I certainly was: concepts like QK- and OV-circuits seemed to make sense algebraically but I was lacking intuition about how they work in practice. In essence, I am aiming to write a post that would have clarified the confusions I had when starting out and that would have given me the intuitions I wish I had.
As part of skilling up on mechanistic interpretability I tackled two of the beginner problems from Neel Nanda’s list of 200 concrete MI problems: exploring how transformers take the max of a list and how they model the Fibonacci sequence. This post starts with a summary of the framework, focusing on the QK- and OV-circuit. Sections 2 and 3 then give a more practical explanation of how these circuits work using examples from the MI problems I worked on. Section 2 is about a single-layer attention-only model which predicts the highest integer from its input sequence as the next token. In this setting we can find the “full” circuits which map from tokens to tokens and can thus be nicely visualized. In the third section I consider a model with a block of fully connected layers (MLP) after the attention block. I explain how the ideas from MFTC can be applied in this setting – this is similar to the derivation of effective weights in A Mechanistic Interpretability Analysis of Grokking.
On terminology: In this post I mainly use “circuit” to denote interpretable, linear subsets of operations in a transformer. This is how the term is used in MFTC to describe the QK- and OV-circuits. More generally, “circuit” is also often used for any subset of a transformer that can be identified as being responsible for a particular task and these circuits are typically non-linear and less interpretable. The type of circuits that I am talking about have also been called “effective weight matrices” since due to their linear nature, they can be seen as connecting distant parts of a model.
On notation:
- Capital letters (A,Q,…) denote matrices.
- Lower case letters (x,t,…) denote vectors.
- A subscript for vectors (xi) denotes that the vector is at position i in the residual stream.
- The superscript h for matrices (Ah) denotes that the operation belongs to a particular attention head h.
- Subscripts for the attention matrix (Ai,j) are used as indices to denote attention from position i to j.
- Square brackets (x[i]) denote that a value is obtained at layer i of a model. In the MFTC paper, xi is sometimes used for this purpose. Since that notation is already used for residual stream positions, I decided to use a different notation.
- Nres is the number of positions in the residual stream, i.e. the context window length of the transformer.
1. A brief overview of the mathematical framework from transformer circuits.
The idea behind the transformer circuit framework is to look for subsets of a transformer’s operations (e.g. multiplication by a weight matrix) that can be understood in isolation and are interpretable. In the language of mechanistic interpretability, such a subset is called a circuit.
What happens in a single-layer attention-only transformer?
To identify circuits, the authors consider a simple transformer with only one layer and no MLP. They formulate equations that describe what happens to a token t (a one-hot encoded vector with length equal to the vocabulary size) at position i in the input sequence, as it is passed through the transformer.

First it goes through the embedding.
(1) xi[0]=WEt
At this point the embedded token enters what is called the residual stream at the position corresponding to the token’s position in the input sequence. Each transformer block features residual connections which add the unchanged input to the output of the attention heads and (if they are included) MLP layers. One way to think of this is that information passes through the transformer in a stream on which the attention heads act by reading and writing. In each transformer block, multiple attention heads h are applied to the block’s input and afterwards the original input is added to their output via the residual connection:
(2) xi[1]=xi[0]+∑h∈Hh(xi[0])
h(xi) for position i in the residual stream is computed as follows:
- Computing the attention pattern A=softmax∗(XTWTQWKX) where X=[x1…xNres] is the matrix of vectors from each position in the residual stream. softmax∗ uses autoregressive masking, meaning that attention from tokens at position i to tokens at position j is set to 0 for j>i. Note that MFTC ignores the scaling of the attention pattern.
- For each position in the residual stream, compute the value vector vi=WVxi.
- A position i‘s result vector ri is then a linear combination of each position j‘s value vector vj, weighted by attention: ri=∑jAi,jvj. Note how Ai,j is a scalar and vj is a vector.
- The output of the attention head at position i is then simply h(xi)=WOri
An important takeaway is that the attention heads are how information travels between positions in the residual stream. The computation of the attention pattern and the result vector are the only time values from different positions in the stream interact. All other operations are between the same position of the stream.
In a typical transformer there would now be an MLP and then more transformer blocks. In our single-layer attention-only toy model, we immediately get the output via the unembedding layer:
(3) T(t)=WUx[1]
You may have noticed that the equations are ignoring layer norms and biases. This is done for the sake of simplicity and should not decrease the frameworks applicability to real transformers. Biases can be simulated in a model without them by appending them to the weights and adding a dimension that is always one to the input vectors: Wx+¯¯b=[W¯¯b][x1]. Something similar, up to a variable scaling, holds for layer normalization.
Introducing the QK and OV circuits
The operations described in the last section fully describe what happens to a token as it passes through a transformer. The transformer circuit paper goes on to rearrange the equations in matrix form to get the following sum in which every term corresponds to an end-to-end path through the model:
T(X)=X(WUWE)T+∑h∈HAhX(WUWhOWhVWE)T
Where A=softmax(XTWTEWTQWKWEX). Note how the embedding and unembedding matrices are now contained within this equation!
The term X(WUWE)T is the direct path from embedding to unembedding. The AhX(WUWhOVWE)T terms are the paths that go through attention heads. The terms on both sides of X can be viewed as independent operations on the input, and if we strip away the non-linear and variable parts (i.e. get rid of the softmax and X) we get two linear operations: WTEWhTQWhKWE and WUWhOWhVWE, often abbreviated as WTEWhQKWE and WUWhOVWE respectively. They can be viewed in isolation from the remaining model and as they map from tokens to tokens they can be relatively easy to interpret. In other words, they are our first two circuits, the QK- and OV-circuit!
The QK-circuit describes attention between tokens at different positions in a head. Remember how the calculation of the attention pattern and result vector are the only operations in a transformer where information travels between positions. The attention pattern is the decisive factor in this mechanism as it determines how much each value vector is weighted when calculating the result vector. In turn, the QK-circuit determines the attention pattern by producing logits for any pair of tokens in the input stream which will be turned into a probability by the softmax. The logit for the attention paid from token t1 to t0 is given by t1WTEWhQKWEt0. MFTC says that in this way the QK-circuit controls which tokens the head prefers to attend to.
Applying Ah to X gives us a linear combination of all residual stream vectors at each position of the stream. Now it is up to the OV-circuit to determine how this linear combination affects the output logits at that position. As an intuition, the QK-circuit can be seen as a mapping from two tokens t1,t2 to the attention t1 pays to t2. In contrast, the OV-circuit can be seen as a mapping from two tokens t1,t2 to the logit of t2 if t1 receives full attention. However, this is not entirely accurate as attention between tokens also depends on their position and neither circuit contains the positional embedding. Hence, the circuits will always return the same values for a given pair t1 and t2 even though the heads behavior might change depending on where the tokens appear in the residual stream.
Initially, it might be a bit unclear what it means for the QK-circuit to “control what tokens are attended to” and the OV-circuit to “determine how attending to a token affects the logits”. This is why I will provide a practical example in the next section, which I hope illustrates how the circuits work in practice.
It should also be noted that the circuits are only so interpretable because we are considering an attention-only model. Adding a MLP complicates the picture as now information can be manipulated between WhO and the unembedding. I will talk more about this case in the third section.
Looking at transformers in terms of circuits opens up a new avenue for interpretability, allowing us to reason about complicated behaviours by looking at how circuits from different layers compose. A given heads’s QK- and OV-circuit has three input channels (WQ,WK and WV) and one output channel (WO) and the output from a head in one layer can compose with each of the three input channels from the next. In two-layer models this famously gives rise to induction-heads which predict that the current token should be followed by whatever came after the previous instance of that token. In models with multiple layers , it makes sense to consider QK- and OV-circuits to be WQK and WOV respectively because circuit-composition happens without the involvement of WE and WU. When the embedding and unembedding are added we speak of a “full” circuit.
2. Practical Example: Taking the max with an attention-only transformer
I trained a number of one-layer attention only transformers to predict the maximum of their input sequence as their next token. The input was a sequence of integers n1n2...nS with the sequence length S between 2 and 6 and each integer between 0 and 63. The size of the residual stream was 32 and since I had one head, it also had a dimension of 32. The remaining architectural and training details, as well as a thorough investigation can be found in this Colab though they are not important for this post.
Before reading on or looking at the Colab, take a moment to think about how a transformer could learn to do this task using the QK- and OV-circuit.
If you already have a good intuitive understanding of what the circuits are doing this may be easy. If not, it might be helpful, to look at the attention patterns for some inputs:
For S=2 and input 52 59:

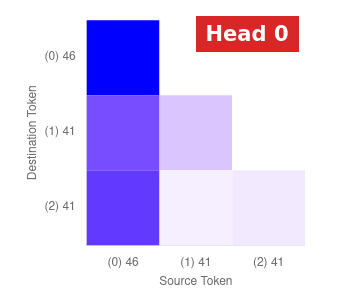
For S=3 and input 46 41 41:
For S=6 and input 35 14 47 61 38 54:

If you are not familiar with the visualization of attention patterns, the diagram shows how much attention the token on the x-axis pays to the token on the y-axis. The axes are marked “(p) n” meaning that the token at position p has value n. We can see that, at the last position, the head has learned to always pay the most attention to whatever is token has the highest cardinality at any position. Since only the output from the last position matters, the attention from the remaining positions is pretty much random. Hence, if we visualize the QK-circuit for the model with S=2 we get…

… something not very interpretable. Remember that the QK-circuit does not take into account the positional encoding. Alas, the position is highly important for the attention pattern in our model and so without it we can’t make sense of the QK-circuit. Fortunately it is quite easy to incorporate the positional encoding into the calculation of the circuit as it is simply added to the embedding: (WTE+WTpos2)WhQK(WE+Wpos1). Let us visualize this transformation with Wpos1 set to the encoding for the last position and Wpos2 for the second-to-last position:

In this plot, the point x,y shows how much attention is paid from token y at position 1 to token x at position 0 (the plot for the attention from 1 to 1 looks similar). We see that tokens of higher cardinality always get more attention. This confirms that there is a general rule behind what we saw in the attention patterns for individual inputs. The amazing thing is that, unlike the attention pattern, we can visualize the QK-circuit for any position without having to pass any data through the model!
So now we know that the QK-circuit “attends” to the token with highest cardinality. How do we expect the OV-circuit to determine the logits based on the attended token? It is not hard to guess that the OV-circuit has to output the highest logit for exactly the token that it is “given” by the QK-circuit. After all, want our transformer to output the highest value from the input sequence and the QK-circuit has already found that value, so all that is left for the OV-circuit is to assign the corresponding logits.
Such an OV-circuit, which assigns the most logits to the selection of the QK-circuit, is called “copying”. In multi-layer transformers we can also speak of copying circuits – if they directly connected to the logits, they can embedd the token in the residual stream. How can we tell if a circuit is copying? One way is to visualize the circuit:

Here, the point x, y shows how much logits are given to token x if token y is attended to by the OV-circuit. The bright diagonal indicates that every token maximizes its own logits. A more general statistic proposed in the framework for transformer circuits is based on the circuit’s eigenvalues. Remember that for a linear transformation X, an eigenvalue is a scalar λ such that there is a vector ¯¯¯v for which X¯¯¯v=λ¯¯¯v. Insofar as the linear transformation is copying we would expect the eigenvalues to be positive, otherwise a token’s contribution to its own logits would be negative. Hence one can use a measure of the eigenvalues’ positiveness such as ∑iλi∑i∥λi∥ as a proxy for how much copying the circuit is doing.
Summing up what we know, we can get a satisfying description of how a max-taking transformer works from our understanding of what the circuits are doing. The QK-circuit selects the token with highest cardinality from all positions and makes the OV-circuit attend that token at the final position. The OV-circuit simply outputs logits that are highest for whatever token it is attending to at the final position.
3. How to stop worrying and analyze the MLP
My goal was to understand a transformer that predicts the next element of a variable input sequence n1n2...nS with 2≤S≤5 so that the next element is always the sum of the two preceding ones, like in the Fibonacci sequence. As the task comes down to doing addition on the last two elements of the input sequence, it seems the most important part is understanding addition and so I first investigated a model with a context-window-length and input sequence size of 2. This model was a single-layer, one-head transformer with an MLP. The vocabulary-size, residual-stream-dimension and hidden-layer-size were all set to 128. Once I understood the addition models, I trained transformers with similar architecture and context-window length 5 to model the Fibonacci sequence and confirmed that the resulting model is using the same addition algorithm and using the positional encoding to make sure the right numbers are added.
The point of this section is not to give a detailed account of my findings, but to illustrate how the circuits we saw in attention-only models can generalize to models with MLPs. If you are still interested in my analysis, you can check out the Colab. In short, it turns out that to do addition the models are at least to a large degree using the same algorithm that Neel Nanda found for modular addition. I found this somewhat surprising as I assumed there would be a simpler way to do regular addition, even for one-hot encodings of tokens. However, I also found some evidence that leads me to believe that the model is also doing something else since a small part of the model’s performance could not be explained using the modular addition algorithm. Ultimately, what I am doing in the Colab is very similar to what Nanda has done for modular addition and because he has already written up such a great in-depth explanation, I do not think it is worth writing about in detail here. Anyway, you need to read neither his work nor my Colab to understand the remaining section.
Circuits in transformer blocks with MLPs
Adding MLPs makes the analysis of transformer blocks much more complicated, both because MLPs themselves are hard to interpret and because of what they do to the circuits. Yet, any reasonably powerful model will feature MLPs so we can not ignore them if we are interested in understanding powerful AI.
In principle, what we want to do is the same as in the attention-only model: identify chunks of what the model is doing that can be interpreted in isolation from the larger model. To do so, we first need to extend the equations from section 1 for a model with an MLP. We can then isolate circuits which I have also seen called “effective weight matrices” in this context.
Let us start by thinking about what happens to an input as we pass it through a one-layer attention+MLP model. How are the applied operations described in section 1 different than in an attention only model? Nothing changes about the embedding and unembedding and so equations (1) and (3) remain the same. The only difference is that after input passes through the attention heads, the residual stream will now be feed into an MLP which also features a skip-connection.

So equation (2) becomes:
(2B) xi[1]=xi[0]+m(xi[0]+∑h∈Hh(xi[0]))
Where m is the MLP function. Typically it features one hidden layer, and assuming we use ReLU activations, m can be defined as:
m(x)=WoutReLU(Winx)
Where Win and Wout are the weights into and out of the hidden layer respectively. Ignoring the residual connection, the term that goes into the ReLU is:
Win∑h∈Hh(xi)=∑h∈H∑Nresj=0WinWhOWhVWExjAhi,j
where Nres is the number of positions in the residual stream (i.e. the size of the contex-window). I appreciate that the terms on the right hand side can look intimidating, so it’s worth taking some time to think about what they mean. Remember how in section 1 we said that the attention head computes for each residual stream position a linear combination of the values from each positions, weighted by attention? This is why we are summing over the xjAhi,j terms where Ahi,j is a scalar that denotes the attention from position i to position j.
Note how WinWhOWhVWE shares three terms with the OV-circuit from the attention-only model. Without the activation function, the MLP would merely result in a larger circuit WUWoutWinWhOWhVWE. But because activations introduce a nonlinearity and we want our circuits to be linear, we can think of the OV-circuit as being “split into two”. This gives us the two “effective weight matrices” Wneur=WinWhOWhVWE and Wlogit=WUWout.
In contrast, the QK-circuit remains unbroken in this new model – the flow of information goes from one position’s token embedding over the attention head towards another position’s embedding and this is independent of if the attention heads are followed by an MLP or not.
Analyzing the addition transformer
This section considers the transformer I trained to do addition which has only one attention head, so I will drop the h superscript.
First, let us see what the QK-circuit is doing:

I used different code for the visualization but the meaning of the plot is the same: How much attention is paid from a token with value given on the y-axis to the values given on the x-axis? This time, only the upper right triangle is relevant to us since the sum of token pairs must be 127 or less (to be within the vocabulary-range of the model). There we see that values are very similar along horizontal lines. This suggests that for any two values, both tokens will be attended with roughly equal attention. This makes sense since addition works the same for any two inputs.
After the QK-circuit has decided what values are attended to, Wneur determines how attended tokens influence the MLP´s neural activations. Can we still get a meaningful visualization of this relation, as we did for the OV-circuit in section 2? Wneur gives a mapping from tokens to hidden layer inputs, without considering attention. This means that if Ai,j=1 for position i, then Wneurxj gives the values of the hidden layer neurons before applying the ReLU when h(xi) is passed into the MLP. Hence, visualizing Wneur gives a heatmap showing how each neuron’s activations vary as full attention is paid to different tokens. This type of visualization can give us an insight into what a single head is doing which suits us just fine since we only have one head. Again, there is the technicality that we have to add the positional encoding to get the true visualization, so really what we want to look at is WinWOWV(WE+Wpos) for each position pos.
For the transformer I trained to do addition that map looks as follows:

(This is for position 1, though 0 looks similar as one would except from commutativity of addition.)
At first glance, the map does not look very interpretable, but it tells us something about the behavior of the different neurons. The vertical lines represent how one neuron’s input changes as a function of the input token. If we look closely at the heatmap it looks there are a lot vertical lines that are dotted in some periodic pattern. To get a better view of what is going on, we can also use Wneur to plot individual neuron inputs:

These activations look suspiciously periodic. Seeing this graph made me suspect that some of the hidden layer’s neurons are modelling trigonometric functions similar to what happens in a model doing modular addition. Further investigation confirmed that this is at least partially the case, but that is beyond the scope of this article. If you are interested in how the tansformer’s algorithm for modular addition works, I recommend you check out this section of the Colab for Neel Nanda’s Analysis of Grokking were he explains it in much greater detail than I do.
I hope this section has demonstrated the role that small circuits {“effective weight matrices”) play in a transformer block. The circuit-framework gives us a way of splitting a large model up into independent parts whose behavior we can identify. Individual parts such as Wneur may do something fairly abstract like modelling trigonometric functions and their purpose may only become clear by looking at the other parts. Yet, by delimiting individual parts in a principled way, the task of understanding the model as a whole has become more tractable.
Final Remarks
For mechanistic interpretability to help with aligning AI we will have to apply it to much larger models. Interpreting such models will be harder in many ways, for example circuits typically will not have useful visualizations.
As I mentioned in the section on terminology, other objects that are called circuits in the literature tend to be larger and less linear. I already mentioned induction heads which form in models with at least two layers and compose two heads. Other examples include a three-layer four-head circuit for Python docstrings and a two-head circuit modeling temporal successor relations. The famous mechanism for detecting indirect objects consists of 26 heads. Still, I believe it is valuable to have a good intuition about the type of work that individual heads can do, even if in practice we may be unable to (and not need to) understand each head of a larger circuit in detail.
If this post got your mouth watering or if your are still confused about how MI actually works in practice, I recommend attempting one of the beginner problems from 200 Concrete Open Problems in Mechanistic Interpretability. Trying things yourself is the best way to learn (and to find out that things are not as difficult as they might seem). Another post that helped make these concepts click for me is Decision Transformer Interpretability which gives similar examples and visualizations for transformers doing Reinforcement Learning.
I believe that Mechanistic Interpretability will be essential in making sure that advanced AI systems are safe. For this purpose, we will need to detect complicated, noisy concepts like deception. Yet, the field currently seems to be nowhere near this capability. But it is also a young field, with many low-hanging fruits to pick and lots of progress to be made.













This post is meant for people who are just getting started with mechanistic interpretability and have an understanding of the transformer architecture as well as the underlying linear algebra. Maybe you have not yet read the mathematical framework for transformer circuits (MFTC) or have read it but are still confused about some things. I know that I certainly was: concepts like QK- and OV-circuits seemed to make sense algebraically but I was lacking intuition about how they work in practice. In essence, I am aiming to write a post that would have clarified the confusions I had when starting out and that would have given me the intuitions I wish I had.
As part of skilling up on mechanistic interpretability I tackled two of the beginner problems from Neel Nanda’s list of 200 concrete MI problems: exploring how transformers take the max of a list and how they model the Fibonacci sequence. This post starts with a summary of the framework, focusing on the QK- and OV-circuit. Sections 2 and 3 then give a more practical explanation of how these circuits work using examples from the MI problems I worked on. Section 2 is about a single-layer attention-only model which predicts the highest integer from its input sequence as the next token. In this setting we can find the “full” circuits which map from tokens to tokens and can thus be nicely visualized. In the third section I consider a model with a block of fully connected layers (MLP) after the attention block. I explain how the ideas from MFTC can be applied in this setting – this is similar to the derivation of effective weights in A Mechanistic Interpretability Analysis of Grokking.
On terminology: In this post I mainly use “circuit” to denote interpretable, linear subsets of operations in a transformer. This is how the term is used in MFTC to describe the QK- and OV-circuits. More generally, “circuit” is also often used for any subset of a transformer that can be identified as being responsible for a particular task and these circuits are typically non-linear and less interpretable. The type of circuits that I am talking about have also been called “effective weight matrices” since due to their linear nature, they can be seen as connecting distant parts of a model.
On notation:
1. A brief overview of the mathematical framework from transformer circuits.
The idea behind the transformer circuit framework is to look for subsets of a transformer’s operations (e.g. multiplication by a weight matrix) that can be understood in isolation and are interpretable. In the language of mechanistic interpretability, such a subset is called a circuit.
What happens in a single-layer attention-only transformer?
To identify circuits, the authors consider a simple transformer with only one layer and no MLP. They formulate equations that describe what happens to a token t (a one-hot encoded vector with length equal to the vocabulary size) at position i in the input sequence, as it is passed through the transformer.
First it goes through the embedding.
(1) xi[0]=WEt
At this point the embedded token enters what is called the residual stream at the position corresponding to the token’s position in the input sequence. Each transformer block features residual connections which add the unchanged input to the output of the attention heads and (if they are included) MLP layers. One way to think of this is that information passes through the transformer in a stream on which the attention heads act by reading and writing. In each transformer block, multiple attention heads h are applied to the block’s input and afterwards the original input is added to their output via the residual connection:
(2) xi[1]=xi[0]+∑h∈Hh(xi[0])
h(xi) for position i in the residual stream is computed as follows:
An important takeaway is that the attention heads are how information travels between positions in the residual stream. The computation of the attention pattern and the result vector are the only time values from different positions in the stream interact. All other operations are between the same position of the stream.
In a typical transformer there would now be an MLP and then more transformer blocks. In our single-layer attention-only toy model, we immediately get the output via the unembedding layer:
(3) T(t)=WUx[1]
You may have noticed that the equations are ignoring layer norms and biases. This is done for the sake of simplicity and should not decrease the frameworks applicability to real transformers. Biases can be simulated in a model without them by appending them to the weights and adding a dimension that is always one to the input vectors: Wx+¯¯b=[W¯¯b][x1]. Something similar, up to a variable scaling, holds for layer normalization.
Introducing the QK and OV circuits
The operations described in the last section fully describe what happens to a token as it passes through a transformer. The transformer circuit paper goes on to rearrange the equations in matrix form to get the following sum in which every term corresponds to an end-to-end path through the model:
T(X)=X(WUWE)T+∑h∈HAhX(WUWhOWhVWE)T
Where A=softmax(XTWTEWTQWKWEX). Note how the embedding and unembedding matrices are now contained within this equation!
The term X(WUWE)T is the direct path from embedding to unembedding. The AhX(WUWhOVWE)T terms are the paths that go through attention heads. The terms on both sides of X can be viewed as independent operations on the input, and if we strip away the non-linear and variable parts (i.e. get rid of the softmax and X) we get two linear operations: WTEWhTQWhKWE and WUWhOWhVWE, often abbreviated as WTEWhQKWE and WUWhOVWE respectively. They can be viewed in isolation from the remaining model and as they map from tokens to tokens they can be relatively easy to interpret. In other words, they are our first two circuits, the QK- and OV-circuit!
The QK-circuit describes attention between tokens at different positions in a head. Remember how the calculation of the attention pattern and result vector are the only operations in a transformer where information travels between positions. The attention pattern is the decisive factor in this mechanism as it determines how much each value vector is weighted when calculating the result vector. In turn, the QK-circuit determines the attention pattern by producing logits for any pair of tokens in the input stream which will be turned into a probability by the softmax. The logit for the attention paid from token t1 to t0 is given by t1WTEWhQKWEt0. MFTC says that in this way the QK-circuit controls which tokens the head prefers to attend to.
Applying Ah to X gives us a linear combination of all residual stream vectors at each position of the stream. Now it is up to the OV-circuit to determine how this linear combination affects the output logits at that position. As an intuition, the QK-circuit can be seen as a mapping from two tokens t1,t2 to the attention t1 pays to t2. In contrast, the OV-circuit can be seen as a mapping from two tokens t1,t2 to the logit of t2 if t1 receives full attention. However, this is not entirely accurate as attention between tokens also depends on their position and neither circuit contains the positional embedding. Hence, the circuits will always return the same values for a given pair t1 and t2 even though the heads behavior might change depending on where the tokens appear in the residual stream.
Initially, it might be a bit unclear what it means for the QK-circuit to “control what tokens are attended to” and the OV-circuit to “determine how attending to a token affects the logits”. This is why I will provide a practical example in the next section, which I hope illustrates how the circuits work in practice.
It should also be noted that the circuits are only so interpretable because we are considering an attention-only model. Adding a MLP complicates the picture as now information can be manipulated between WhO and the unembedding. I will talk more about this case in the third section.
Looking at transformers in terms of circuits opens up a new avenue for interpretability, allowing us to reason about complicated behaviours by looking at how circuits from different layers compose. A given heads’s QK- and OV-circuit has three input channels (WQ,WK and WV) and one output channel (WO) and the output from a head in one layer can compose with each of the three input channels from the next. In two-layer models this famously gives rise to induction-heads which predict that the current token should be followed by whatever came after the previous instance of that token. In models with multiple layers , it makes sense to consider QK- and OV-circuits to be WQK and WOV respectively because circuit-composition happens without the involvement of WE and WU. When the embedding and unembedding are added we speak of a “full” circuit.
2. Practical Example: Taking the max with an attention-only transformer
I trained a number of one-layer attention only transformers to predict the maximum of their input sequence as their next token. The input was a sequence of integers n1n2...nS with the sequence length S between 2 and 6 and each integer between 0 and 63. The size of the residual stream was 32 and since I had one head, it also had a dimension of 32. The remaining architectural and training details, as well as a thorough investigation can be found in this Colab though they are not important for this post.
Before reading on or looking at the Colab, take a moment to think about how a transformer could learn to do this task using the QK- and OV-circuit.
If you already have a good intuitive understanding of what the circuits are doing this may be easy. If not, it might be helpful, to look at the attention patterns for some inputs:
For S=2 and input 52 59:
For S=3 and input 46 41 41:
For S=6 and input 35 14 47 61 38 54:
If you are not familiar with the visualization of attention patterns, the diagram shows how much attention the token on the x-axis pays to the token on the y-axis. The axes are marked “(p) n” meaning that the token at position p has value n. We can see that, at the last position, the head has learned to always pay the most attention to whatever is token has the highest cardinality at any position. Since only the output from the last position matters, the attention from the remaining positions is pretty much random. Hence, if we visualize the QK-circuit for the model with S=2 we get…
… something not very interpretable. Remember that the QK-circuit does not take into account the positional encoding. Alas, the position is highly important for the attention pattern in our model and so without it we can’t make sense of the QK-circuit. Fortunately it is quite easy to incorporate the positional encoding into the calculation of the circuit as it is simply added to the embedding: (WTE+WTpos2)WhQK(WE+Wpos1). Let us visualize this transformation with Wpos1 set to the encoding for the last position and Wpos2 for the second-to-last position:
In this plot, the point x,y shows how much attention is paid from token y at position 1 to token x at position 0 (the plot for the attention from 1 to 1 looks similar). We see that tokens of higher cardinality always get more attention. This confirms that there is a general rule behind what we saw in the attention patterns for individual inputs. The amazing thing is that, unlike the attention pattern, we can visualize the QK-circuit for any position without having to pass any data through the model!
So now we know that the QK-circuit “attends” to the token with highest cardinality. How do we expect the OV-circuit to determine the logits based on the attended token? It is not hard to guess that the OV-circuit has to output the highest logit for exactly the token that it is “given” by the QK-circuit. After all, want our transformer to output the highest value from the input sequence and the QK-circuit has already found that value, so all that is left for the OV-circuit is to assign the corresponding logits.
Such an OV-circuit, which assigns the most logits to the selection of the QK-circuit, is called “copying”. In multi-layer transformers we can also speak of copying circuits – if they directly connected to the logits, they can embedd the token in the residual stream. How can we tell if a circuit is copying? One way is to visualize the circuit:
Here, the point x, y shows how much logits are given to token x if token y is attended to by the OV-circuit. The bright diagonal indicates that every token maximizes its own logits. A more general statistic proposed in the framework for transformer circuits is based on the circuit’s eigenvalues. Remember that for a linear transformation X, an eigenvalue is a scalar λ such that there is a vector ¯¯¯v for which X¯¯¯v=λ¯¯¯v. Insofar as the linear transformation is copying we would expect the eigenvalues to be positive, otherwise a token’s contribution to its own logits would be negative. Hence one can use a measure of the eigenvalues’ positiveness such as ∑iλi∑i∥λi∥ as a proxy for how much copying the circuit is doing.
Summing up what we know, we can get a satisfying description of how a max-taking transformer works from our understanding of what the circuits are doing. The QK-circuit selects the token with highest cardinality from all positions and makes the OV-circuit attend that token at the final position. The OV-circuit simply outputs logits that are highest for whatever token it is attending to at the final position.
3. How to stop worrying and analyze the MLP
My goal was to understand a transformer that predicts the next element of a variable input sequence n1n2...nS with 2≤S≤5 so that the next element is always the sum of the two preceding ones, like in the Fibonacci sequence. As the task comes down to doing addition on the last two elements of the input sequence, it seems the most important part is understanding addition and so I first investigated a model with a context-window-length and input sequence size of 2. This model was a single-layer, one-head transformer with an MLP. The vocabulary-size, residual-stream-dimension and hidden-layer-size were all set to 128. Once I understood the addition models, I trained transformers with similar architecture and context-window length 5 to model the Fibonacci sequence and confirmed that the resulting model is using the same addition algorithm and using the positional encoding to make sure the right numbers are added.
The point of this section is not to give a detailed account of my findings, but to illustrate how the circuits we saw in attention-only models can generalize to models with MLPs. If you are still interested in my analysis, you can check out the Colab. In short, it turns out that to do addition the models are at least to a large degree using the same algorithm that Neel Nanda found for modular addition. I found this somewhat surprising as I assumed there would be a simpler way to do regular addition, even for one-hot encodings of tokens. However, I also found some evidence that leads me to believe that the model is also doing something else since a small part of the model’s performance could not be explained using the modular addition algorithm. Ultimately, what I am doing in the Colab is very similar to what Nanda has done for modular addition and because he has already written up such a great in-depth explanation, I do not think it is worth writing about in detail here. Anyway, you need to read neither his work nor my Colab to understand the remaining section.
Circuits in transformer blocks with MLPs
Adding MLPs makes the analysis of transformer blocks much more complicated, both because MLPs themselves are hard to interpret and because of what they do to the circuits. Yet, any reasonably powerful model will feature MLPs so we can not ignore them if we are interested in understanding powerful AI.
In principle, what we want to do is the same as in the attention-only model: identify chunks of what the model is doing that can be interpreted in isolation from the larger model. To do so, we first need to extend the equations from section 1 for a model with an MLP. We can then isolate circuits which I have also seen called “effective weight matrices” in this context.
Let us start by thinking about what happens to an input as we pass it through a one-layer attention+MLP model. How are the applied operations described in section 1 different than in an attention only model? Nothing changes about the embedding and unembedding and so equations (1) and (3) remain the same. The only difference is that after input passes through the attention heads, the residual stream will now be feed into an MLP which also features a skip-connection.
So equation (2) becomes:
(2B) xi[1]=xi[0]+m(xi[0]+∑h∈Hh(xi[0]))
Where m is the MLP function. Typically it features one hidden layer, and assuming we use ReLU activations, m can be defined as:
m(x)=WoutReLU(Winx)
Where Win and Wout are the weights into and out of the hidden layer respectively. Ignoring the residual connection, the term that goes into the ReLU is:
Win∑h∈Hh(xi)=∑h∈H∑Nresj=0WinWhOWhVWExjAhi,j
where Nres is the number of positions in the residual stream (i.e. the size of the contex-window). I appreciate that the terms on the right hand side can look intimidating, so it’s worth taking some time to think about what they mean. Remember how in section 1 we said that the attention head computes for each residual stream position a linear combination of the values from each positions, weighted by attention? This is why we are summing over the xjAhi,j terms where Ahi,j is a scalar that denotes the attention from position i to position j.
Note how WinWhOWhVWE shares three terms with the OV-circuit from the attention-only model. Without the activation function, the MLP would merely result in a larger circuit WUWoutWinWhOWhVWE. But because activations introduce a nonlinearity and we want our circuits to be linear, we can think of the OV-circuit as being “split into two”. This gives us the two “effective weight matrices” Wneur=WinWhOWhVWE and Wlogit=WUWout.
In contrast, the QK-circuit remains unbroken in this new model – the flow of information goes from one position’s token embedding over the attention head towards another position’s embedding and this is independent of if the attention heads are followed by an MLP or not.
Analyzing the addition transformer
This section considers the transformer I trained to do addition which has only one attention head, so I will drop the h superscript.
First, let us see what the QK-circuit is doing:
I used different code for the visualization but the meaning of the plot is the same: How much attention is paid from a token with value given on the y-axis to the values given on the x-axis? This time, only the upper right triangle is relevant to us since the sum of token pairs must be 127 or less (to be within the vocabulary-range of the model). There we see that values are very similar along horizontal lines. This suggests that for any two values, both tokens will be attended with roughly equal attention. This makes sense since addition works the same for any two inputs.
After the QK-circuit has decided what values are attended to, Wneur determines how attended tokens influence the MLP´s neural activations. Can we still get a meaningful visualization of this relation, as we did for the OV-circuit in section 2? Wneur gives a mapping from tokens to hidden layer inputs, without considering attention. This means that if Ai,j=1 for position i, then Wneurxj gives the values of the hidden layer neurons before applying the ReLU when h(xi) is passed into the MLP. Hence, visualizing Wneur gives a heatmap showing how each neuron’s activations vary as full attention is paid to different tokens. This type of visualization can give us an insight into what a single head is doing which suits us just fine since we only have one head. Again, there is the technicality that we have to add the positional encoding to get the true visualization, so really what we want to look at is WinWOWV(WE+Wpos) for each position pos.
For the transformer I trained to do addition that map looks as follows:
(This is for position 1, though 0 looks similar as one would except from commutativity of addition.)
At first glance, the map does not look very interpretable, but it tells us something about the behavior of the different neurons. The vertical lines represent how one neuron’s input changes as a function of the input token. If we look closely at the heatmap it looks there are a lot vertical lines that are dotted in some periodic pattern. To get a better view of what is going on, we can also use Wneur to plot individual neuron inputs:
These activations look suspiciously periodic. Seeing this graph made me suspect that some of the hidden layer’s neurons are modelling trigonometric functions similar to what happens in a model doing modular addition. Further investigation confirmed that this is at least partially the case, but that is beyond the scope of this article. If you are interested in how the tansformer’s algorithm for modular addition works, I recommend you check out this section of the Colab for Neel Nanda’s Analysis of Grokking were he explains it in much greater detail than I do.
I hope this section has demonstrated the role that small circuits {“effective weight matrices”) play in a transformer block. The circuit-framework gives us a way of splitting a large model up into independent parts whose behavior we can identify. Individual parts such as Wneur may do something fairly abstract like modelling trigonometric functions and their purpose may only become clear by looking at the other parts. Yet, by delimiting individual parts in a principled way, the task of understanding the model as a whole has become more tractable.
Final Remarks
For mechanistic interpretability to help with aligning AI we will have to apply it to much larger models. Interpreting such models will be harder in many ways, for example circuits typically will not have useful visualizations.
As I mentioned in the section on terminology, other objects that are called circuits in the literature tend to be larger and less linear. I already mentioned induction heads which form in models with at least two layers and compose two heads. Other examples include a three-layer four-head circuit for Python docstrings and a two-head circuit modeling temporal successor relations. The famous mechanism for detecting indirect objects consists of 26 heads. Still, I believe it is valuable to have a good intuition about the type of work that individual heads can do, even if in practice we may be unable to (and not need to) understand each head of a larger circuit in detail.
If this post got your mouth watering or if your are still confused about how MI actually works in practice, I recommend attempting one of the beginner problems from 200 Concrete Open Problems in Mechanistic Interpretability. Trying things yourself is the best way to learn (and to find out that things are not as difficult as they might seem). Another post that helped make these concepts click for me is Decision Transformer Interpretability which gives similar examples and visualizations for transformers doing Reinforcement Learning.
I believe that Mechanistic Interpretability will be essential in making sure that advanced AI systems are safe. For this purpose, we will need to detect complicated, noisy concepts like deception. Yet, the field currently seems to be nowhere near this capability. But it is also a young field, with many low-hanging fruits to pick and lots of progress to be made.