Exploring Simon’s Algorithm

December 2024
M	T	W	T	F	S	S
	1
2	3	4	5	6	7	8
9	10	11	12	13	14	15
16	17	18	19	20	21	22
23	24	25	26	27	28	29
30	31

Simon’s algorithm provided the first example of an exponential speedup over the best known classical algorithm by using a quantum computer to solve a particular problem. Originally published in 1994, Simon’s algorithm was a precursor to Shor’s well-known factoring algorithm, and it served as inspiration for many of the seminal works in quantum computation that followed.

Daniel Simon: “A bit of amusing history: I submitted my algorithm to a theoretical computer science conference (STOC 1993), but it was rejected. However, Peter Shor was on the program committee for that conference, and immediately saw the potential (that I had had absolutely no inkling of, to be honest) for applying the same general algorithm structure to concrete problems like factoring and discrete logarithms. After trying unsuccessfully to persuade the committee to accept my paper, he got to work on his own, and submitted it to the next major theoretical computer science conference (FOCS 1993)—in parallel with mine, resubmitted. We had in fact agreed to merge the papers if only his was accepted, but the committee fortunately agreed to accept them both, giving us each credit for our respective portions of the resulting achievement.”

Simon’s problem:

Simon’s algorithm was designed to solve a particular mathematical problem:
Suppose we’re given a function f:{0,1}ⁿ→{0,1}ⁿ that maps bit strings to bit strings. We’re also given the promise that the function f either maps each unique input to a unique output, or maps two distinct inputs to one unique output, but we’re not told which. Mathematically, this means that f is either one-to-one or two-to-one, and that we are given the promise

$Simon's problem promise: for all x and y in {0,1}^n, f(x)=f(y) if and only if x=y oplus s$

for some unknown n-bit string s∈{0,1}ⁿ, and where ⊕ means bitwise addition modulo 2.

Said another way, there exists an unknown string s such that, for all input strings x, f(x)=f(x⊕s). When s is non-zero, the function is two-to-one as it maps exactly two inputs to every unique output. When s is the zero string, the function is one-to-one.

The goal of Simon’s algorithm is to determine if f is one-to-one or two-to-one, which we will do by directly finding the secret string s. As a matter of fact, it can be shown that finding s is mathematically equivalent to solving the original question in the oracle setting we are considering here.

Daniel Simon: “This algorithm solves a “promise problem”: a function is provided in the form of an oracle that has a particular promised property, and the algorithm extracts some related property out of the function, provided that the promise is fulfilled. This is a natural target for quantum algorithms, because “quantum parallelism” allows functions to be explored across an exponential space of inputs. Deutsch and Jozsa were the first to suggest this approach to demonstrating a gap between quantum and classical algorithms, but their attempt, while exponentially faster for quantum algorithms than for deterministic classical ones, is in fact easily solved (with exponentially small error probability) by a classical probabilistic algorithm.”

Classical complexity

To solve Simon’s problem classically, one needs to find two different inputs x and y for which f(x)=f(y), since one can then determine s=x⊕y (where addition is done bitwise, mod 2), or otherwise show that no two inputs produce the same output.

Daniel Simon: “This might not be true—it’s possible that there’s some magic algorithm that can always find the string s efficiently, by somehow rooting around in the details of the computation of f. However, we abstract away such hypothetical solutions—which are almost never found, but also almost never proven impossible—by expressing f as an oracle, which leaves finding an actual pair of inputs with the same output as the only path to finding s.”

How hard is it to find two distinct inputs that map to the same output, given the function f as a black box? For n-bit strings, there are 2ⁿ possible inputs. Thus, in the worst case, one would need to check at most 2ⁿ different inputs to find a pair that maps to the same output; this provides an upper bound on the required query complexity. How about a lower bound? Classically, it can be shown that we need to check Θ(2^n/2) inputs, which still scales exponentially in the size of the problem. The intuition behind this lower bound comes from the (generalized) birthday problem: within a group of people, what is the probability that two of them share the same birthday? One can turn this problem around and ask “how many people do we need in a room to ensure that the probability that at least two of them share a birthday is greater than some fixed number?” It turns out that you need a number of people given by roughly the square root of the number of possible birthdays (i.e., 365). For Simon’s problem, this means you need to check about Θ(2^n/2) inputs.

Quantum algorithm for Simon’s problem

Simon’s algorithm is a scheme for solving the preceding problem using exponentially fewer queries to the function f. In order for Simon’s algorithm to work, one needs to be able to implement the unknown function f using quantum logic. In other words, we need a unitary operator U_f that encodes the action of the function f as a transformation on quantum states. Specifically,

For our purposes, we can safely assume that the unitary U_f is given to us as a black box (an “oracle”), and that we don’t know how it works, but we do know that it implements the preceding transformation. One benefit of the oracle model is that we don’t need to know how the oracle works — we just have to trust that it does. The Simon’s Algorithm notebook provides an implementation of a commonly used example oracle for f, as well as a detailed explanation of how and why it works.

Quantum circuit

Daniel Simon: “The quantum circuit and quantum Turing machine models are equivalent, but we didn’t know this back when this algorithm was created, and it was conceived in the quantum Turing machine setting. Yao demonstrated the equivalence of the two models shortly afterwards.”

Simon’s algorithm involves both quantum and classical components. The quantum part of Simon’s algorithm is used to query the oracle efficiently, while the classical component is used to process measurement results and determine the hidden string s. A circuit for the quantum component of Simon’s algorithm is shown here.

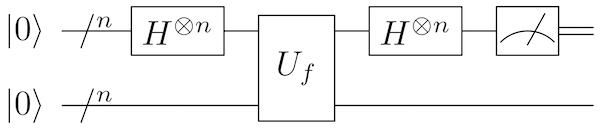
Quantum circuit for Simon's algorithm. Hadamard gates are applied to the first n qubits, then the oracle unitary U_f is applied to all 2n qubits. Then another round of Hadamard gates to the first n qubits. Finally, the qubits are measured.

Daniel Simon: “The most striking thing about this circuit is its simplicity—in fact, it’s even simpler than the original Deutsch-Jozsa circuit that was first proposed as a possible demonstration of the power of quantum computation. Indeed, this simple algorithm preceded the corresponding problem: I began by trying (perhaps somewhat foolishly) to prove that classical computations could simulate quantum ones, and this circuit design was the simplest I could find that resisted straightforward classical simulation. So I began to explore its properties, and eventually built a problem around it tailored to its simulation-resistant behavior.”

For a function f acting on n-bit strings, the circuit above acts on 2n qubits, as needed for the definition of U_f. Only the first n qubits need to be measured; the remaining qubits are unused after the application of U_f.

The mathematical details

In order to understand how this quantum circuit solves the problem with exponentially fewer queries to the function f than a classical algorithm, we need to dive a bit deeper into the math.

To solve Simon’s problem, one needs to run the quantum circuit above several times. After each run of the circuit, the measurements of the first n qubits produce an output bit string, which we denote by z.

An analysis of the circuit above shows that each output bit string z satisfies the following condition:

Let’s see why this is the case, by analyzing the above circuit step-by-step. Full mathematical details for these steps are available in the accompanying notebook.

1. Initialize all qubits in the |0⟩ state.
2. Apply Hadamard gates to each of the first n qubits, placing them in the equal superposition state.
3. Apply the oracle U_f, which computes the function f into the last n qubits.
4. Measure the last n qubits, giving a random result f(x). If f is one-to-one, this output of f corresponds to an input of x. If f is two-to-one, the output of f corresponds to an input of either x or y=x+s, where x and y are the two different inputs to f that gave the same output f(x)=f(y). Note that this step is not strictly necessary, since we do not need the measurement result, but we include it as it makes the analysis easier.

Daniel Simon: I certainly envisioned executing this step—it would have been a lot harder to think through the algorithm without this simplification…

1. Apply Hadamard gates to each of the first n qubits. If f is one-to-one, the state |x⟩ is mapped to

$Applying Hadamard gates to the n qubit state ket x = square root of 1/2^n times sum over x in {0,1}^n of (-1)^(x dot z) ket z$

where x·z is the dot product between the two strings represented as vectors (modulo 2).

Daniel Simon: It took me a while to recognize this characterization of the phase produced by the Hadamard gate, which was key to extracting interesting information from the algorithm. When I first presented the algorithm to Ethan Bernstein and Umesh Vazirani at Berkeley, before it was published, I proudly pointed out this key fact, and Umesh quickly nodded and said “yes”, bearing the annoyed look of someone who’s just had a junior researcher point out something painfully obvious to him. Evidently, they’d been aware of this observation for a while, and simply hadn’t spotted how to exploit it.

Similarly, if f is two-to-one, the state (|x⟩+|y⟩)/√2 is mapped to

$1/square root of 2^(n+1) times sum over x in {0,1}^n of [(-1)^(x dot z) + (-1)^(y dot z)] ket z$

1. Measure the first n qubits.
  If f is one-to-one, measurements return a random bit string z uniformly chosen from {0,1}ⁿ.
  If f is two-to-one, measurements return a random bit string z such that x·z=y·z mod 2, since otherwise the amplitude (−1)^(x·z)+(−1)^(y·z) cancels out. Using the criterion for Simons problem (f(x)=f(y)⟹x=y⊕s), we find that

Series of equation manipulations showing the condition that s dot z = 0 mod 2

Thus, in both cases we obtain a random bit string z such that s·z=0.
Therefore, each time we run the quantum circuit above, we find a bit string z that is orthogonal to the secret string s.

Daniel Simon: I was originally looking for a way to distinguish between general one-to-one and two-to-one functions. However, I got stuck because s — the exclusive-or of two colliding inputs — varies arbitrarily for a general two-to-one function. Eventually, it occurred to me to make s constant across the function by defining it as the “promise” in a promise problem, and the result followed.

Classical post-processing

From the measurement results {z₁,…,z_k}, we can form a system of equations: {z_k·s=0 mod 2}.

set of equations z_j dot s = 0 mod 2 for j from 1 to k

There are k equations and n unknowns (the elements of s). If we run the quantum part enough times so that we find n independent equations, then we can solve these equations (using, for example, Gaussian elimination) to recover the secret string s. This is precisely the classical post-processing required: solve the system of equations found above to recover the string s. If you’re interested in deeper details, refer to the appendix of the notebook.

Quantum complexity

Running the above quantum circuit O(n) times is sufficient to give n linearly independent equations, which we can use to solve for s. Therefore, Simon’s algorithm can be solved using O(n) queries to U_f. Since the classical algorithm requires Ω(2^n/2) queries, this establishes an exponential speedup of the quantum algorithm.

Implementation on Amazon Braket

We first import a method called simons_oracle implemented in the amazon-braket-examples repository. This method implements a particular quantum oracle for a secret function f. We explain this specific function and its quantum implementation in the notebook appendix. The simons_oracle method accepts a secret string s, which we choose at the start. Our goal is to recover this same string s.

# Implemented in NBI / example notebook utils from simons_utils
import simons_oracle

s = '101011' # Secret string

n = len(s) 
circ = Circuit()
# Apply Hadamard gates to the first n qubits
circ.h(range(n))
# Apply the Oracle for f. See NBI / notebook for implementation
circ.simons_oracle(s)
# Apply Hadamard gates to the first n qubits 
circ.h(range(n))

print(circ)

This code snippet generates the following circuit:

T   : |0|     1     | 2 |3|4|5|6|
                                 
q0  : -H-C-----------C---C-C-C-H-
         |           |   | | |   
q1  : -H-|-C---------|-H-|-|-|---
         | |         |   | | |   
q2  : -H-|-|-C-------|-H-|-|-|---
         | | |       |   | | |   
q3  : -H-|-|-|-C-----|-H-|-|-|---
         | | | |     |   | | |   
q4  : -H-|-|-|-|-C---|-H-|-|-|---
         | | | | |   |   | | |   
q5  : -H-|-|-|-|-|-C-|-H-|-|-|---
         | | | | | | |   | | |   
q6  : ---X-|-|-|-|-|-X---|-|-|---
           | | | | |     | | |   
q7  : -----X-|-|-|-|-----|-|-|---
             | | | |     | | |   
q8  : -------X-|-|-|-----X-|-|---
               | | |       | |   
q9  : ---------X-|-|-------|-|---
                 | |       | |   
q10 : -----------X-|-------X-|---
                   |         |   
q11 : -------------X---------X---

T   : |0|     1     | 2 |3|4|5|6|

We now run the circuit using the Amazon Braket local simulator 4n times. We choose the number of shots to be 4n so that, with high probability, we will obtain at least n linearly independent samples that we can use to solve for s.

# Sets the device to run the circuit on
device = LocalSimulator()
# Run the circuit 4n times, should be sufficient to get n independent bit strings
task = device.run(circ, shots=4*n)

And that’s it! The rest of the algorithm is purely classical. As explained in the preceding classical post-processing section, these measurement outcomes define a set of linear equations, which we can solve to recover the classical string s. If you want to run the full example yourself, you can find the code in the Simon’s Algorithm notebook in the Amazon Braket examples repository. The examples in this repository also come preinstalled on Amazon Braket notebooks to help you get started quickly.

Conclusion

Simon’s algorithm was a key contribution to the early foundations of quantum information theory and quantum computation. Today, this algorithm is often taught to students of quantum information theory as part of the core curriculum, since its simple implementation can be covered in the span of a single lecture. However, the simplicity of the algorithm belies its significance, as the conceptual ideas discovered in Simon’s algorithm can also be found through a number of today’s advanced quantum algorithms.