This is a bonus Part 3 to Quantum Algorithm Untangled’s series on the Deutsch-Jozsa Algorithm. Part 1, which introduces the Problem and explains the reasons behind each step of the algorithm, can be found here. Part 2, which explores the mathematics and how to implement each part of Deutsch-Jozsa, can be found here.

Now, we’ve seen just how powerful Quantum Computing is, with the Deutsch-Jozsa Algorithm’s incredible O(1) run-time complexity.
However, Deutsch-Jozsa doesn’t really do a lot. In fact, the problem seems awfully specific, as if crafted to play to Quantum Computers’ strengths. Not that this makes the algorithm ‘bad’ per se — it still shows the incredible potential of Quantum Computing — but still, let’s look at a more general, albeit complex version. One that solves a much more difficult problem with a still-amazing speedup. One that could even potentially have real-world applications in cryptography.

Let’s explore the Bernstein-Vazirani Algorithm.

Introduction

The Bernstein-Vazirani Problem:

Just like with Deutsch-Jozsa, we’ll eventually model this using an Oracle. So, while explaining the rules of the Problem, let’s go back to our Quantum Game Show analogy, with the host laying out the rules of the game.

“Here is a list of numbers. You can choose any of them, and hand it to me.
In return, I’ll tell you ‘0’ or ‘1’.”

“Similar to Deutsch-Jozsa so far, but here’s the twist. I’m thinking of one, very specific number in that list, and I’ll tell you the inner product of your number and mine, with modulo 2 (don’t worry, we’ll explain this soon!). This will be that zero or one.

“You have to guess the exact number I’m thinking of to win. There’s only one right answer, out of all those possible numbers.”

“Which number am I thinking of? Can you guess it?”

The Classical Algorithm:

Once again, let’s translate this into something a computer can do.

Our guess, from a list of numbers, is our Query from a particular input domain.

The host, again, is our Black Box Oracle. This Oracle holds a hidden bit string (the number we are trying to guess), and uses it in their operation.

The output, again, is ‘0’ or ‘1’. It’s the result of the Oracle’s function.

But what is that function? The ‘inner product of the Query and the hidden bit string, with modulo 2’. Let’s dissect this.

First, what’s a inner product? It’s a concept from Linear Algebra — 3b1b’s video and the mathsisfun page (the example without using cos) do an excellent job at explaining a dot product. Inner products are just like dot products — except they continue the same process for more than just 2 numbers. Here’s a good resource for it — once again, the example without cos.
In short, we take a single element from both vectors, and multiply them. Take the next two elements, multiply them, and add the result to the previous number. Take the next two, multiply, and add to the running total, and so on.

It might seem unclear how exactly it relates to our situation, though. Inner Products involve two vectors, and we’re just working with numbers, aren’t we?

Well, we’re working with binary numbers. Let’s use an example, working from the Oracle’s perspective. The hidden bit string is ‘01101’, and our Query is ‘10101’.

So how do we map these to vectors? Quite simply, all we have to do is take each binary digit as an element, and write the vectors out.

We can’t take the inner product of two row vectors, though — as explained in the last link, we’ll need take the transpose of the first vector. Just change it from a column to a row vector, and keep everything else the same.

Then multiply each element, and add to get a result of 2.

Interestingly, only (1×1) will ever return 1 in the multiplication stage; all other combinations return 0. This matches up with the Truth Table for the Classical AND Gate, meaning this can be exactly represented by AND Gates. It’s nothing essential to the process, but an intriguing idea nonetheless.

Now, the modulo by 2.

Now what’s a modulo operation? It’s remarkably simple — just a remainder. Dividing 10 by 3, for example, goes 3 times with a remainder of 1. So, 10 mod(3) = 1. Easy as that.

2 mod(2) = 0, so our Oracle would output zero. If, our input had been something like ‘01000’, it would have output ‘1’. Feel free to calculate how.

The Classical Solution

Drawing this as an algorithm gives us our usual circuit.

Now, we only get a single bit of Output to work with. Logically, this means each time we query the Oracle, we can get a single bit of information at most about the hidden bit string.

Because of this, we want to avoid wasting any of those bits, and get rid of any ambiguity. We need an input which can, with 100% certainty, determine one bit of the answer.

Remember that ‘01000’ Query from earlier? Think about why it output 1.

Because the ‘1’ in the Query matched up with a ‘1’ in the answer, we got an output of 1 mod(2) = 1. Every other Query bit was 0, and so would have simply added 0 to the answer — so this could not have been 3 mod(2).
If we had gotten a 0 as output, then we know our ‘1’ didn’t match up with a ‘1’ in the hidden bit string. There must have been a zero in that spot.

So, we know for sure that we have a ‘1’ in the answer, in the second position.

The Classical Algorithm simply repeats this process for every bit! For a string of length 5, like our example, that means ‘10000’, ‘01000’, ‘00100’, ‘00010’, and ‘00001’.

At that point, we are guaranteed to know the answer — the number of Queries equals the length of the list. Thinking back to Big-O Notation, that’s O(n) time, and won’t scale very well for massive lists.

The Quantum Algorithm

The Bernstein-Vazirani Algorithm is surprisingly similar to the Deutsch-Jozsa Algorithm we’re already experienced with, showing similar O(1) complexity and using similar quantum properties. In fact, you have an inkling as to how to convert Deutsch-Jozsa into this new problem.
If you do, try to take a few minutes aside — maybe with a paper and pencil — and try to figure out how to tweak Deutsch-Jozsa to suit Bernstein-Vazirani. Follow the same process as we did when creating our Deutsch-Jozsa Algorithm. What’s our algorithm going to look like? What quantum properties do we want to exploit? How do we go about doing that? Which inputs and outputs do we want, and which Quantum Gates create the right Oracle for us? How will we smuggle information out of that Oracle by exploiting those gates? Finally, how do we turn this information into a correct answer?

Then, by all means, continue to see how well you’ve done. It’s always good to try to take steps like these; someday, it might be you creating these miraculous algorithms!

Alright then. Let’s get down to business. First, let’s draw up our general Quantum Circuit, taking care that it’s reversible.

While we’re at it, let’s create the Qiskit environment we’ll be working in. We’ll handle imports and initialise our Circuit.

n = 5   #the size of the Query and hidden bit stringcircuit = q.QuantumCircuit(n+1,n) #initialise circuit, with extra
                                  #Auxiliary qubit 

You might note that we have one less classical bit than qubit — good observation! That’s because we don’t actually need to measure the Auxiliary; we’ll go into detail why later on.

Next up, we should figure out which Quantum properties we’ll be exploiting. Luckily, it’s no different from Deutsch-Jozsa — superposition and Phase Kickback are our friends!

Superposition is easy enough to do. Let’s simply loop through our Query, applying a Hadamard Gate to each Query qubit.

for i in range(0,n):
    circuit.h(i)    #Hadamard on entire Query

Here’s where we are so far.

We can’t quite figure out Phase Kickback just yet — we need to know what gates the Oracle contains, so that we can find the right eigenvector to use. So let’s get on that.

What do we want our Oracle to do? It’s always best to be extremely clear about this before creating it.

The Oracle needs to do 4 things:

1. Contain a random, n-bit hidden bit string. In our case, n=5.
2. Take in two inputs, the Query and Auxiliary.
3. Calculate the inner product of the hidden bit-string and Query mod(2) without affecting the Query, and set the Auxiliary to that value.
4. Output the Query and Auxiliary output.

Let’s handle the first two stages quickly, defining our Oracle function. It’ll take in the Query and Auxiliary through the ‘circuit’ argument, and the value of n through ‘n’.

We’ll also use our trick from last time to generate a random binary string of n digits, so that we have no idea which one the Oracle uses. Also, just for drawing purposes, let’s include a barrier.

def Oracle(circuit,n):
    hidden_bits = randint(0,2**n-1) #random n-digit number
    hidden_bits = format(hidden_bits,'0'+str(n)+'b') #binary convert
    circuit.barrier()

Now, let’s break down Stage 3 into what needs to happen at each step. Let’s look at the Truth Table for each individual multiplication between the first bits, using our examples of hidden bit string ‘01101’ and Query ‘10101’.

We take the ‘0’ and the ‘1’, and multiply them together. Since there’a a zero present, we don’t add anything to our final result.
For the ‘1’ and ‘0’ afterwards, we have the same result.
After that, we get two ‘1’s. This means we add 1 to the result, changing our ‘0’ Auxiliary to a ‘1’.
Two zeros follow, and we do nothing to the Auxiliary.
Another two ones, so we add 1 again, rising to 2. Keeping in mind our mod(2), though, this actually changes the ‘1’ back to a ‘0’.

Hmm. So we’re flipping our Auxiliary between ‘0’ and ‘1’. Isn’t that rather reminiscent of an X-Gate? Combine that with the fact that the ‘flipping’ depends upon our Query, and that sounds awfully like our favourite 2-Qubit Gate, the Controlled-X. It fulfils all of our requirements, just like in Deutsch-Jozsa!

The CX Gate clearly links the Query with the output — if the Query bit is equal to 1, add to the Auxiliary by flipping it. So how do we represent the hidden bit string? How do we make sure that, if the hidden bit string is 0, even if the Query’s 1, the Auxiliary will be unaffected?

Think about what’s controlling the Auxiliary. It’s the combination of a Query in the ‘0’/‘1’ state, and the presence of a CX Gate.
So, we can exert influence over the Auxiliary with the Query and CX Gate, and we need to influence it with the Query and hidden bit string. Just like we can turn the Query ‘on’ and ‘off’ with the binary value, we need to turn the CX Gate ‘on’ and ‘off’.
How do we stop the CX Gate working? By not including it in the first place!

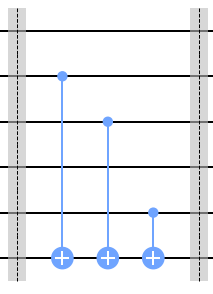
We can look at each bit of the hidden bit string. If that bit is a ‘0’, then no need to add a CX Gate; just pass over that bit. If it’s a ‘1’, then we’ll use the CX Gate on the corresponding bit of the Query and Auxiliary.

for i in range(n):    if hidden_bits[i] == '0':
        pass
    elif hidden_bits[i] == '1':
        circuit.cx(i,n+1)    #if hidden bit is 1, CX on 
                             #corresponding Query and Auxiliary

Now all we need to do is close off the Oracle with a barrier, and return the circuit. We’ll also return the hidden bit string, so we can check if the algorithm works later on.

circuit.barrier()return circuit,hidden_bits

We’re not quite done with this section yet, though. We’ve still got to handle Phase Kickback.

Now that we know our Oracle uses CX Gates, we know which eigenvector we’ll need to use to get our eigenvalue of -1, and ‘smuggle’ out information.

If what I just said makes no sense, I’d recommend you take a peek at this exact same situation in Deutsch-Jozsa, where I’ve explained it in full. Conveniently, it’s all at the section labeled ‘Phase Kickback’.

tl;d: We’ll need to initialise our Auxiliary in the ‘ — ‘ state. This causes Phase Kickback to kick the eigenvalue ‘-1’ onto the Control qubit, the Query, and leaving a mark. The ‘mark’ is Relative Phase, which leaves the measurement probabilities of the circuit unchanged, and the circuit fully reversible — but sets qubits that went through a CX Gate as different to those that didn’t.

Setting this ‘ — ‘ state up is simple enough — before we add our Oracle to the Circuit, we’ll set up our Auxiliary with an X and Hadamard Gate, which puts us perfectly into the right state. Check the link if you don’t know why; the Hadamard Truth Table should help you out.

circuit.x(n+1)
circuit.h(n+1)  #initialise Auxiliary into |-> for Phase Kickbackcircuit,hidden_bits = Oracle(circuit,n)

Now, let’s look at the Output our Oracle gives us.

Obviously, there’s our Auxiliary, holding information about that inner product mod(2) operation. Hooray!
Just kidding — forget about the Auxiliary. It’s got a single bit of information, but we want to reconstruct the entire hidden bit thing. The Auxiliary does very little to help us in that regard.

Instead, our Query holds the golden ticket. You might have cottoned on to what’s going on here; it’s the exact same thing as in Deutsch-Jozsa!

Phase Kickback only affected the ‘1’ component of the Query, and therefore the superpositions underwent a shift in Relative Phase. Once again, if this soudns a bit iffy, check the link to Deutsch-Jozsa. It’s all there.

Any Query which passed through a CX Gate had its state flipped like so:

Here, the CX Gate ‘kicked back’ that -1 eigenstate, but only onto the ‘1’ state which activated it. This flipped the state from ‘+’ to ‘ — ‘.

Just like Deutsch-Jozsa, we’ve smuggled out our information. Any qubit that interacted with a CX Gate has the ‘ — ‘ state, whereas any qubit that did not would still be in the ‘+’ state.

So, again like Deutsch-Jozsa, we apply a Hadamard to all of these qubits. Any qubit in the ‘ — ‘ state transforms into the ‘1’ state, and those in ‘+’ transform to the ‘0’ state . If we measure all of the Query, we’ll know exactly which qubit did which option. Qubits in the ‘1’ state must have gone through the CX Gates, and so represent the positions of the ‘1’s in the hidden bit string!

for i in range(n):
    circuit.h(i)   #take all qubits out of superposition 
    circuit.measure(i,i)   # and measure

The last thing we have do to with our Quantum Circuit is set up our simulation of it.

This is pretty much the exact same story as last time — since we’re running on Qiskit’s BasicAer simulator, our circuit will be 100% accurate, so no need to build in any error-correction or use multiple shots. We just need to set up BasicAer’s qasm_simulator, remembering to set memory=True.

simulator = qiskit.BasicAer.get_backend('qasm_simulator')
job = qiskit.execute(circuit, simulator, shots=1, memory=True)
result = job.result()
measurements = result.get_memory()[0]   #e.g '10110'

Remember that Qiskit flips our output. We measured the top bit of the Query first, so that’s the last digit of measurements. Don’t forget to flip it back around!

Now, how do we translate this output into the verdict of our hidden bit string?

The only way to obtain a ‘1’ state would have been to be in the ‘ — ‘ state before the final Hadamard. All other qubits would have remained in the ‘+’ state, and become ‘0’ during the Hadamard.
The only way to get into that ‘ — ‘ state would have been during Phase Kickback from a CX Gate mid-circuit, since all other qubits would stay in the ‘+’ state.
The only qubits that went through Phase Kickback were those that were in the ‘1’ position of the hidden bit string.

So, if we shorten that all:

The qubits in the ‘1’ state mark a ‘1’ position in the hidden bit string. Those in the ‘0’ state mark a ‘0’.

That’s that — our output (after being reversed) is equal to our hidden bit string! Of course, we’ll compare just to be sure.

measurements = measurements[::-1] #reverse stringprint(f'The Hidden Bit String was {hidden_bits}.')
print(f'The prediction was {measurements}.'if hidden_bits == measurements:
    print('Correct!')

Circuit complete!

The Complete Code

Note: As before, to utilise circuit.draw('mpl') you would want to use a Jupyter Notebook (.ipynb) rather than Python file (.py)

To use real Quantum Computers, we only need to differ slightly from our previous example with Deutsch-Jozsa, which you can find here.

#running 
from qiskit.tools.monitor import job_monitor qiskit.IBMQ.load_account() 
provider = qiskit.IBMQ.get_provider('ibm-q') 
backend = provider.get_backend('ibmq_athens')
 
job = qiskit.execute(circuit,backend,shots=1024) 
job_monitor(job) 
result = job.result() noisy_measurements = result.get_counts()    #returns dictionary, 
                                    #with output string as keys
                              #and count as the respective value  
#get the result which occurred the most 
measurements = max(noisy_measurements, key=noisy_measurements.get)

In fact, only two parts of the procedure change: now, we’ll flip the entire string ‘measurement’ to account for Qiskit reversing the measurement output; and, we’ll use our output to solve the Bernstein-Vazirani problem, not Deutsch-Jozsa.

#flip measurements to account for Qiskit's style
measurements = measurements[::-1]print(f'The Hidden Bit String was {hidden_bits}.')
print(f'The prediction was {measurements}.'if hidden_bits == measurements:
    print('Correct!')

However, we do actually have to slightly alter the Circuit we created — our Bernstein-Vazirani uses a 5-qubit Query plus an Auxiliary.
Most of IBM-Q’s systems only have 5 qubits; ibmq_melbourne could handle all 6, but there’s a massive queue of people wanting to use its extra qubits. It’ll be faster to just change ’n’ to 4 when running this circuit, and use another system like ibmq_athens. Of course, you can use whichever system you like, as long as it has enough qubits.

n = 4

Here’s the new program in full, with a 4-qubit Query and running on a Quantum Computer (ibmq_athens) instead of BasicAer’s qasm_simulator.

And that’s everything! You just solved the Bernstein-Vazirani Problem in O(1) time — demonstrating, once again, the sheer power of Quantum Computing. Hopefully now you have a good sense for what happens; feel free to read over anything that doesn’t make sense, or leave a response here if you’ve got any questions or feedback!

Now that you’ve seen two Quantum Algorithms, perhaps you’re beginning to figure out what Quantum Computing is all about. That’s great! The first step to delving into the field of Quantum Computing is complete!

Both Deutsch-Jozsa and Bernstein-Vazirani are very similar, however, both mainly exploiting Phase Kickback. So, in two weeks, we’ll take a look at another algorithm. One that’s slightly more complex, but vastly more useful — Grover’s Algorithm. We’ll take a look at some other ways we can exploit the quantum world, and achieve speed-ups that put classical computers to shame.